Reconstruction Case Study: Blue River, CO

Introduction
The Blue River, Colorado case study provides a closer look at the steps that were taken to generate one particular
tree-ring reconstruction of annual streamflow. It is important to note that while different investigators may make different choices in their reconstruction approach, these choices are made within
a common framework. The steps listed below outline a common sequence of tasks involved in reconstructing climate from tree rings:
- Evaluating the available tree-ring data and gaged flow data
- Calibrating a set of tree-ring data with the flow data to generate a reconstruction model
- Validating the model
- Evaluating the calibration and validation statistics
- Applying the model to the full length of the tree-ring data to generate the final
reconstruction
The Blue River is a major tributary of the upper Colorado River, and is a main water supply for Denver Water and also a component of the Colorado-Big Thompson Project. The streamflow record for the Blue River above Dillon Reservoir is one of a set that Denver Water uses to characterize their historic and current water supply. The "natural flow" record used in this reconstruction was derived by Denver Water from the raw gage record to account for diversions and transfers of water. The record begins in 1916, and the annual flow values are for the standard water year, October through September.
(Note: Since this Case Study was written up, an updated reconstruction was generated for the Blue River at Dillon. It covers the period 1437-2002, compared to 1440-1999 for the reconstruction described in the Case Study. The updated reconstruction for the Blue River at Dillon is archived in TreeFlow, not the reconstruction described below--although the steps used to derive the two reconstruction are nearly identical.)
Evaluation of data characteristics
The first step in reconstructing streamflow from tree-ring data is to assess the suitability of both the tree-ring data and the streamflow data for the reconstruction. The strength of the relationship between tree growth and streamflow are assessed, as is the shape of the relationship. The statistical characteristics of both the tree-ring and streamflow data are also evaluated.
Strength of relationship. The strength of the relationship between the available tree-ring chronologies and the streamflow data is evaluated in terms of the correlation coefficient, R, which quantifies the variance shared by the two records. In our tree-ring collection efforts, we specifically target moisture-sensitive trees, whose growth responds to the same regional climate patterns that control streamflow. Consequently, nearly all chronologies in western Colorado are significantly and positively correlated (lower growth = lower flow; higher growth = higher flow) with the Blue River gage record and other records in the upper Colorado River basin. Using tree-ring chronologies that have a plausible physical relationship to streamflow (as indicated by a significant correlation) helps prevents a model based on spurious relationships.
Shape of relationship. Simple scatterplots of tree-ring chronologies versus streamflow are used to assess the linearity of the relationship between tree growth and flow. The statistical method used in most reconstructions, multiple linear regression, specifically applies to linear relationships. If a linear relationship is not evident in the plots, data can be transformed to make the relationship linear (e.g., streamflow is sometimes transformed using a log transformation) In this case, scatterplots of tree-ring chronologies against the Blue River gage data showed the relationships to be generally linear, so no transformation was required.
Statistical characteristics of the data. The multiple linear regression technique used in the reconstruction process also requires that a number of assumptions about the data be met in order to obtain unbiased, efficient, and consistent estimates from the model. These assumptions are ultimately tested by evaluating the errors (also called residuals) in the reconstruction model--that is, the difference between the gaged and estimated values. Checking the input data to evaluate the extent to which they meet these assumptions prior to generating the model helps ensure that the resulting model errors will also meet the assumptions (or, if there are problems meeting the assumptions, may point to a cause).
These assumptions are that:
- (1) Values are normally distributed
- (2) Values are independent of each other (no significant autocorrelation)
- (3) Values (streamflow only) vary constantly over time (no significant trends or changes in variance)
Histograms of both the tree-ring and streamflow data showed the data to be normally distributed. The "standard" tree-ring chronologies, however, usually contain statistically significant low-order autocorrelation (that is, one year's growth is strongly related to the next). Most of this autocorrelation is a function of the trees' physiology, and not related to climate. We removed the low-order autocorrelation in the tree-ring chronologies using autoregressive-moving-average (ARMA) modeling. These "residual" chronologies were then used in the reconstruction model. Finally, the streamflow data was found to have sufficiently constant variance over time.
Calibrating the reconstruction model
The statistical process we used to generate the Blue River flow reconstruction model is called a stepwise multiple linear regression, a form of least-squares regression. The tree-ring chronologies (the independent variables, or predictors) are calibrated with gage data (the dependent variable, or predictand) in such a way as to minimize the difference between estimated and true gage values (these differences or errors are squared, thus the smallest squared errors, or least squares, are sought). The stepwise process determines which predictors from a pool of possible candidate predictor chronologies provides a statistical model that best fits the gage data. In the simplest terms, the process first selects the predictor/chronology that explains the most variance in the gage record, then adds the chronology that explains the most variance in the gage record not already explained by the first, and so on, until the remaining unexplained variance cannot be significantly reduced by any of the remaining chronologies. The resulting regression equation--the weighted linear combination of chronology values--is used to estimate the gage value for each year, in this case, 1916-1999.
This stepwise regression process requires a pool of candidate predictor variables, which have been evaluated for suitability as described above. In this case, the pool included all of our chronologies from western Colorado that are sensitive to moisture and that extend at least through 1999 (25 total at the time the reconstruction was generated). All of these chronologies would be expected to potentially contribute to explaining the variance in the Blue River gage record.
One consideration in the selection of chronologies for the predictor pool is the length of the chronology. The length of the final reconstruction is typically limited by the shortest chronology that contributes to it. If a reconstruction should extend back to a certain year (e.g, 1550), then chronologies starting after 1550 should be excluded from the pool of candidate predictors. For the Blue River reconstruction, no chronology was excluded from the predictor pool on the basis of length, and the shortest predictor chronology, Montrose (MTR) begins in 1440. Thus, the reconstruction begins in 1440.
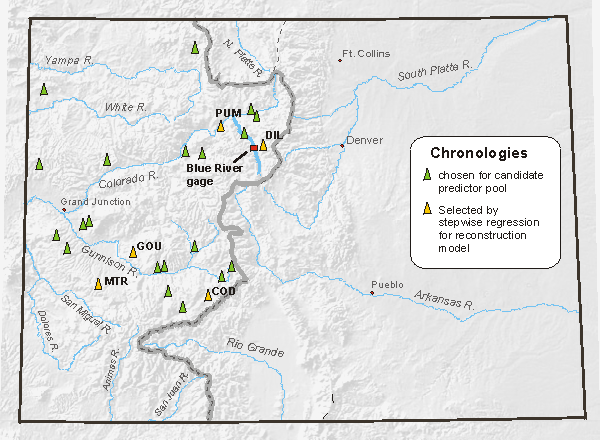
The locations of the chronologies entered into the stepwise regression process (green and yellow), the chronologies selected by the regression as predictors in the reconstruction model (yellow), and the Blue River gage. Note that the predictor chronologies are not necessarily located in the same basin as the gage--reflecting the regional coherence of climate variability--though the chronology (DIL) explaining the most variance in the gaged record is, in fact, the one closest to the gage.
In the calibration, a stepwise linear regression is run for the full set of years common to both the tree-ring and gage data. For the Blue River calibration, the steps in the regression process are shown in the table below:
Summary of Stepwise Regression
| Predictor | Step | Cumulative R | Cumulative R2 | Change in R |
| DIL | 1 | .691 | .477 | .477 |
| PUM | 2 | .749 | .561 | .084 |
| COD | 3 | .771 | .594 | .033 |
| GOU | 4 | .778 | .605 | .011 |
| MTR | 5 | .791 | .626 | .021 |
Here, the chronology that explains the most variance in the Blue River gage record is Dillon (DIL). This chronology explains almost 48% of the variance by itself (Change in R2 ). Pump House (PUM) contributes another 8%, and the remaining three add between 1% and 3%, together explaining 62.6% of the variance in the gaged record.
It is important to limit the number of predictors in the regression model, by imposing a significance threshold for additional predictors to be entered into the equation, ending the process at a predetermined number of steps, or assessing the change in the reduction of error (RE) statistic as additional predictors enter the model. A model with a large number (>8-10) of predictors may be "overfitted" to the gage data; the model will be so highly tuned to the calibration period that it is unlikely to perform well during the reconstruction period.
The summary of the final regression model is shown below. The multiple correlation coefficient, R, indicates the amount of shared variance between the tree-ring chronologies in the model and the streamflow record. The R2, as mentioned above, is the amount of variance explained or accounted for by the regression model. The F statistic, which takes into account both the sample size and number of predictors, indicates that the regression equation has a very strong correlation with the gaged record; the probability of that relationship resulting from chance alone is about 1 in 500 quadrillion. The standard error of the estimate, the variation in the error, is 37,419 acre-feet.
The bottom part of the table contains details of the regression model, including the coefficients (or weights) of the predictors and the Y-Intercept. BETA values are standardized coefficients, and B values are non-standardized. The t statistic is equivalent to the F statistic and tests the significance of each of the predictor variables. None have more than 4% probability that their fit to the remaining variance is due to chance alone.
Regression Summary
R= .791 R²= .626
F(5,78)=26.138 p<.00000 Standard Error of estimate: 37419.
| B (Coefficient) | Std. Error of B | t | p-level | |
| Y-Intercept | 49642.0 | 19772.88 | 2.51061 | .014121 |
| DIL | 74039.9 | 14702.88 | 5.03574 | .000003 |
| PUM | 62346.5 | 19466.66 | 3.20273 | .001971 |
| COD | 27425.1 | 12537.54 | 2.18744 | .031706 |
| GOU | 50232.9 | 22045.50 | 2.27860 | .025427 |
| MTR | -40977.8 | 19465.38 | -2.10516 | .038496 |
The errors (or residuals) in the regression model were then examined to make sure assumptions of multiple linear regression, as outlined above, were not violated. Plots of the residuals for the Blue River model showed no violations of these assumptions. Also, residuals were not correlated with any individual predictor variable, one additional assumption.
Validation of the model
After the model is generated, the skill of the model is tested using a set of validation statistics. There are a number of ways to go about validating the model (or comparing several competing models to select the best). Ideally, the model is validated using independent data, i.e., gage data completely withheld from the calibration process. But since gaged streamflow records in Colorado and the West are only 50-100 years long at best, withholding enough data from the calibration to independently validate the model (at least 30 years) significantly shortens the calibration period, and thus can reduce the range of values upon which the model is calibrated.
Here, all available gage data were used in the calibration, and a split-sample validation was used, which tests reconstruction skill of the predictor chronologies selected in the stepwise process. This approach is based on splitting the period of time common to the tree-ring and gaged data into two or more subsets, then calibrating the model on one part and estimating the values for the remaining data. Two extremes of this approach are ( 1) splitting the common period in half, calibrating on one half and testing the model on the other half and then switching the calibration/verification periods or (2) calibrating on all but one case, estimating that case, then removing a different case, and estimating that one, repeating until each case has been omitted and estimated (sometimes called "leave-one-out" or PRESS method). This is more properly known as cross-validation and does not test the regression model per se. Instead, it assesses the ability of the set of predictor chronologies to estimate streamflow using different subsets of the data, and then tests these estimates on the withheld portion of the data.
In the Blue River reconstruction, the approach of splitting the common time period into halves did not work well because the halves of the streamflow record had notably different variance, range of values, and mean. Instead, we used the PRESS method. At each regression run, one case was omitted and estimated until each case had been estimated, generating a time-series of independently estimated values.
Model validation statistics compare the observed gage record to the series of individually estimated cases, called the validation series. Statistics reported are the reduction of error (RE), and the root mean squared error (RMSE). The RE tests the skill of the regression model in estimating the gage values relative to a prediction based on no knowledge (the mean of the calibration period for the gage record is used as "no knowledge"). The RE can be treated as the validation series equivalent of the explained variance in the original regression (R2). The RMSE (root mean squared error) is a measure of the average size of the prediction error for the validation series. It is given in the original units of the gage data, and can be compared to the standard error of the estimate in the original regression.
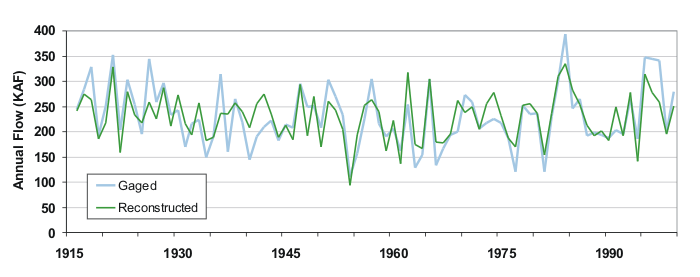
Gaged (blue) and reconstructed (green) records for Blue River flow over the calibration/validation period (1916-1999). Note that the fit between the two records is poorest during the 1930s; the features of this decade are generally not captured well by trees in western Colorado.
One result inherent to the least-squares regression process is that reconstructions have reduced variance relative to the gaged record, so that wet extremes are often underestimated, and dry extremes, often overestimated. Wet extremes also tend to be underestimated because of tree physiology; in years when moisture is sufficiently plentiful (such as 1983-84, above), the trees' growth may not respond to additional inputs of moisture. But overall, the trees reproduce both the year-to-year variability and decadal-scale trends in streamflow very well.
Evaluating the Calibration/Validation Statistics
In evaluating the reconstruction models, the higher the explained variance (R2) in the calibration, and the smaller the standard error, the better, but the validation statistics are needed both to demonstrate that the regression is not overly tuned to the calibration data, and to provide a more robust assessment of the quality of the reconstruction model. The validation statistics are based on data not used in the calibration or, in the case of the LNN, on an iterative method that uses randomly selected cases. To evaluate the quality of the reconstruction, compare the similarity of
- (1) the explained variance for the calibration (R2), and the equivalent for the validation series (RE),
- (2) the standard error of the estimate (calibration error), and the RMSE (the error for the validation series)
The calibration and validation statistics for the Blue River model are reported below, based on the years 1916-1999:
| Statistic | Calibration | Validation |
| Explained variance (R2) | 0.63 | |
| Reduction of Error (RE) | 0.56 | |
| Standard Error of the Estimate | 37,419 AF | |
| Root Mean Square Error (RMSE) | 39,108 AF |
The statistics based on the validation are lower than the calibration statistics, showing decreasing skill--as would be expected when tested on independent data--but the decrease is relatively modest. Tree-ring reconstructions that explain 50% or more of the variance in the instrumental record are considered good, particularly if the validation's explained variance is also 50% or more. Here, about 63% of the variance in the Blue River gage is explained by the full calibration model, and the validation statistics indicate that at least 56% of the variance is accounted for when the predictors are tested on validation data. The Blue River reconstruction is considered a high-quality reconstruction.
Generating the Reconstruction
Once the model is calibrated and validated, the predictor chronologies and their regression coefficients are used to reconstruct estimates of streamflow for the years of the tree-ring chronologies. This is done by entering the chronologies' values into the regression equation and calculating the estimated streamflow for each year. For the Blue River reconstruction, the regression equation is:
Blue River gage estimates = 49642.0 + DIL(74039.9) + PUM (62346.5) + COD (27425.1) + GOU (50232.9) - MTR (40977.8).
Each of the five chronologies extends at least to 1440, so the full reconstruction is 1440-1999.
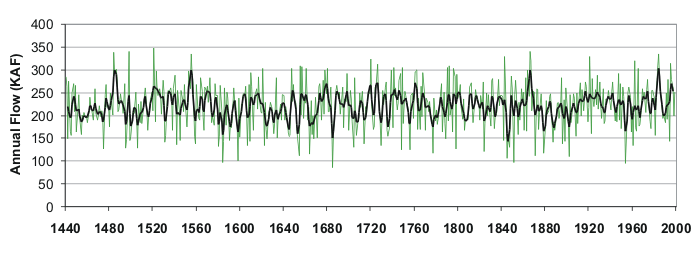
The full reconstruction of the Blue River above Dillon Reservoir flow record, with annual values (green) and a 5-year weighted mean (black)
Uncertainty and estimating the confidence interval
Because the reconstruction model explains most--but certainly not all--of the variance in the gage record, there is uncertainty in the reconstructed values. Estimates of uncertainty can be described by confidence intervals (CIs) around the reconstruction. These confidence intervals describe the range of uncertainty (usually at a 95% level) that can be expected in the estimates. There are several way to estimate confidence intervals. The most straightforward way is to use the root mean squared error (RMSE) from the regression validation to calculate the confidence interval.
The RMSE is equivalent to the standard deviation (1 sigma) from the distribution of validation errors. So if we add the RMSE to each reconstructed flow value, and also subtract the RMSE from each reconstructed flow value, these two time series would form the upper and lower bounds of the 68% (+/- 1 sigma) confidence interval. To instead generate the 95% confidence interval, we would first multiply the RMSE by 1.96 before adding/subtracting this value from each reconstructed flow value. And to generate the 80% confidence interval, we would first multiply the RMSE by 1.282 before adding/subtracting this value from each reconstructed flow value.
Analyzing the reconstruction
The extended streamflow reconstructions generated from tree rings provide a basis for many different analyses that may be useful to water resource management. Several examples of such analyses are described below. It is important to recognize that these results are for one gage (the Blue River above Dillon Reservoir) and one reconstruction, and these specific results should not be applied elsewhere. Although similar results are found for other gages in the Upper Colorado, reconstructed drought years do vary somewhat, as a consequence of local differences, quality of the gaged data, and uncertainties in the reconstruction model.
Long-term assessment of modern drought events
Tree-ring reconstructions of streamflow allow gaged drought events, such as the extreme 2002 drought, to be assessed in a much longer context than afforded by the gage record itself. At most Colorado stream gages, including the Blue River, 2002 was the lowest flow year on record. The 560-year reconstruction for the Blue River contains six years with reconstructed flows lower than the 2002 gaged flow: 1584, 1598, 1685, 1845, 1851, and 1954 (see figure below). The reconstruction actually underestimates the flow for 1954, which is the second driest year in the gage record, after 2002. Because the reconstruction contains some uncertainty--the tree-ring data do not explain all the variance in the gage record--it is also necessary to consider this when assessing the rarity of the 2002 event. When this uncertainty is taken into consideration, we find 26 years (including those listed above) which may have equaled or exceeded the severity of 2002.
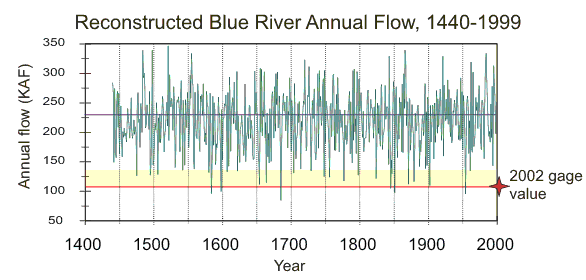
Reconstructed annual flow for the Blue River, 1440-1999 (green), with the 2002 gage value projected as a red line and the uncertainty (at 95% confidence) in the reconstruction about that value shown as a yellow band.
Many water managers considered 2002 to be the third year of a three-year drought. When considered as a three-year event, this drought is much less rare. In the Blue River gage record (1916-1999) alone, the cumulative severity of 2000-2002 was exceeded six times, most recently in 1975-1977. The reconstruction confirms this three-year drought as being unexceptional, with 48 three-year droughts exceeding 2000-2002, even without considering the uncertainty in the reconstruction.
Changes in distribution of drought years
Reconstructions of streamflow show the temporal distribution of extreme low flow years over past centuries. When Blue River reconstruction annual values are color-coded to show percentiles of flow, patterns of wet and dry years can be assessed (see figure below). Years in the lowest 10th percentile are marked with red ovals to show how these years are distributed over the past 560 years. Percentiles are calculated on the basis of ranking years by flow values. For example, the driest 10% of years are the 56 years in the 0 to 10th percentiles.
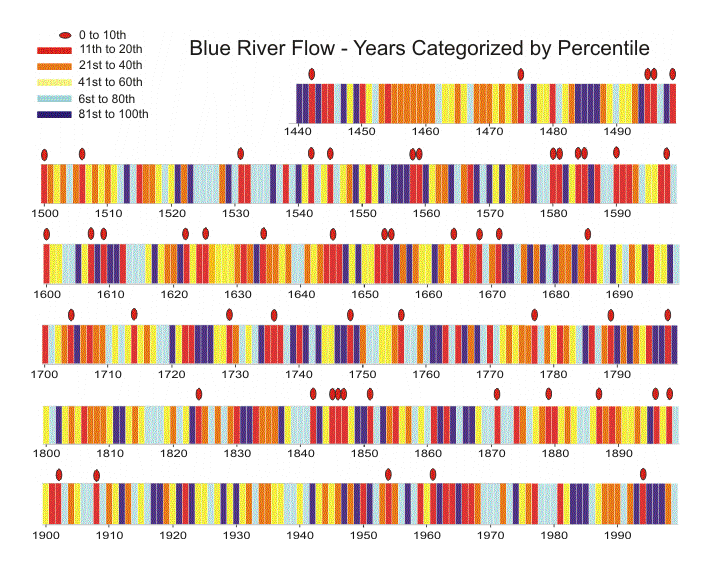
In the 20th century, there were only five years with flow in the lowest 10th percentile, fewer than in any other century. In all other full centuries except the 18th century, more than double this number occurred (19th - 11, 18th - 9, 17th - 13, 16th - 13, 1440-1499 - 5). In addition, there are several instances of back-to-back extreme dry years, most notably the three-year sequence 1845-47. This figure also shows sequences of years when flow was below the 40th percentile for many consecutive years. For example, for nine years, 1453-1461, no flows were above the 40th percentile. This reconstruction also shows that many extremely dry years are preceded or followed by very wet years. The period from 1580 to 1588 contains two sets of two consecutive extremely dry years, but both sets are followed by a very wet year. This representation of the Blue River reconstruction make it clear that there has been a great deal of variability in streamflow over the past 5 centuries.
Years preceding and following drought events
Tree-ring reconstructions of streamflow can be used to evaluate the types of years that tend to precede and follow extremely dry years. The single years immediately preceding and following an extremely dry year (driest 10th percentile) can be categorized into five equal classes, based on the color-coded classes described in the previous figure.
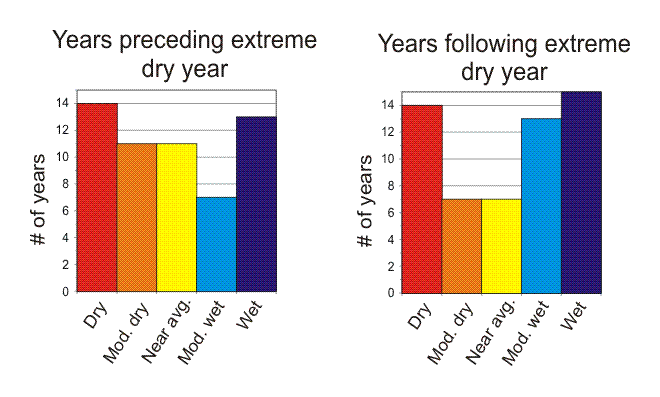
For the Blue River, the years preceding extremely dry years show a slight tendency to be drier than average. In contrast, years following extremely dry years tend to be wet or moderately wet, although there is a secondary peak of dry years.
Again, these tendencies are for the record of flow in the past. They may provide some guidance as to what to expect in the future, but it is important to note that the reconstructions cannot be used as predictive tools. The climate of the past is likely not an analogue to the climate of the future because of human impacts on climate in the 20th century, which will doubtlessly continue into the future. The tree-ring reconstructions of steamflow provide a record of natural hydroclimatic variability over which humanimpacts on climate will be superimposed.



