San Joaquin River inflow to Millerton Lake
The San Joaquin River is an important input into the California State Water Project, operated by the California Department of Water Resources (CDWR). In 2013-2014, David Meko and Ramzi Touchan (University of Arizona Laboratory of Tree-Ring Research) developed a reconstruction of the San Joaquin River, and along with a reconstruction for the San Joaquin River, Four Rivers Index for the CDWR.
References:
Klamath/San Joaquin/Sacramento Hydroclimatic Reconstructions, Final Report to CADWR from Tree Rings
Methods
Water-year-total flows for the San Joaquin were reconstructed by locally weighted regression, or Loess from subsets of 61 chronologies screened for Sacramento/San Joaquin basin reconstructions. A Loess reconstruction was defined as an interpolation of estimated flow from a smoothed scatterplot of observed flow on a single summary tree-ring variable. The tree-ring predictor was an average standard chronologies that were filtered and scaled to accentuate their statistical signal for the target flow gage. A time-nested-modeling approach was used for reconstructions, using progressively longer but smaller subsets of chronologies going back in time to calibrate subsets of reconstrutions. The percentage of flow variance accounted for by the “median-accuracy” model ranges from 68% for the Sacramento River (Sacramento River above Bend Bridge) to 78% for the San Joaquin River. Because these reconstructions are done with time-nested models, accuracy varies over time depending on the quality of the available tree-ring chronologies.
| Statistic | Calibration | Validation |
| Explained variance (R2) | 0.78 | |
| Reduction of Error (RE) | 0.76 | |
| Standard Error of the Estimate | 438 KAF | |
| Root Mean Square Error (RMSE) | 458 KAF |
Note: the calibration and validation statistics above were computed during the model development and reflect the relationship between the log-transformed observed flows and the tree-ring predictors. The scatterplot below in Figure 1 shows the relationship between the back-transformed observed flows and the reconstructed flows, which has a lower R2 than that reported in the table. Also, the Standard Error of the Estimate and Root Mean Square Error reported above are in log units, and the RMSE can't be used to compute the confidence intervals.
(For explanations of these statistics, see this document (PDF), and also the Reconstruction Case Study page.)
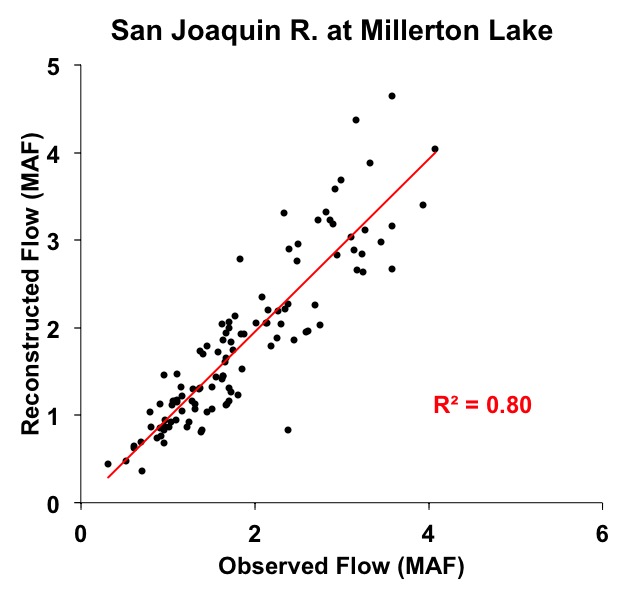
Figure 1. Scatter plot of observed and reconstructed San Joaquin River annual flow, 1901-2012.
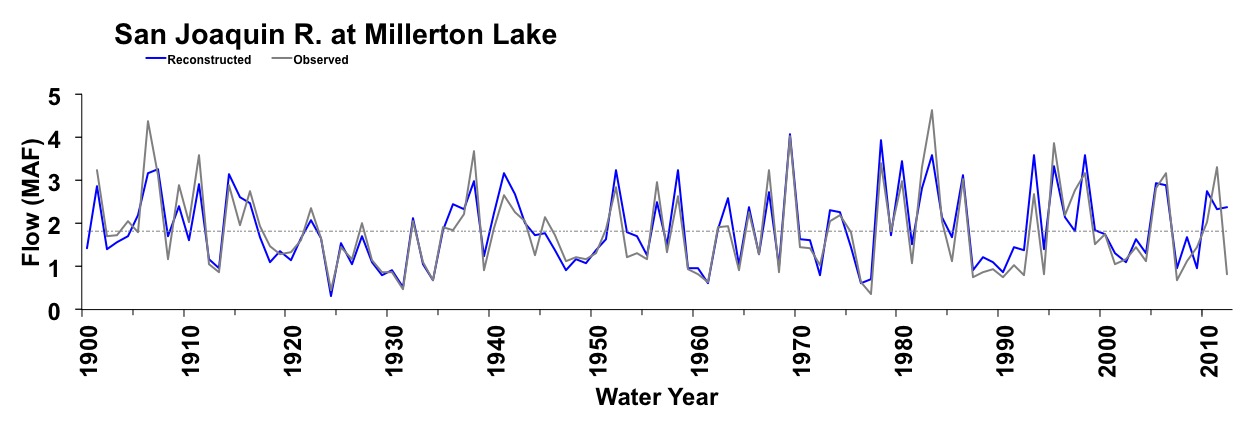
Figure 2. Observed (black) and reconstructed (blue) annual San Joaquin River annual flow, 1901-2012. The observed mean is illustrated by the dashed line.
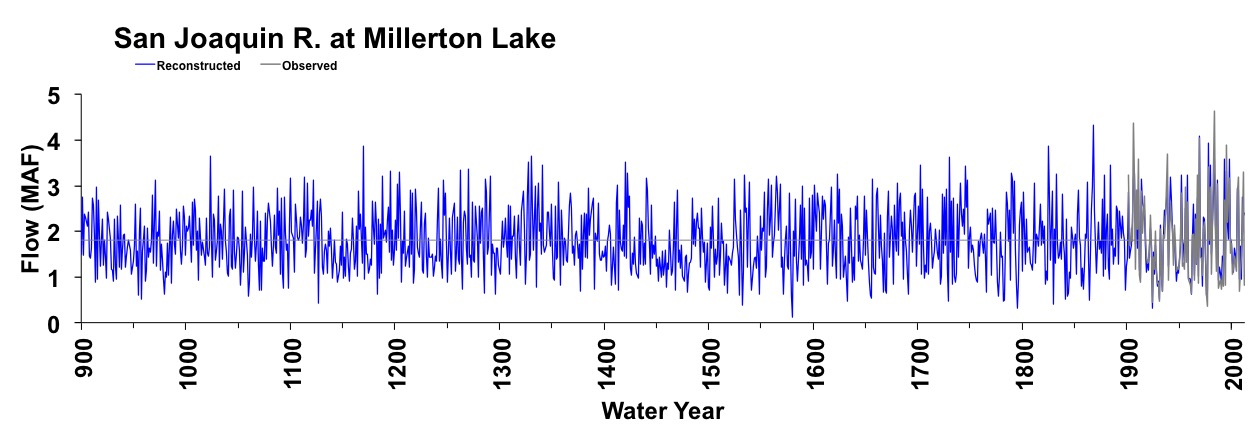
Figure 3. Reconstructed annual flow for the San Joaquin River (900-2012) is shown in blue. Observed flow is shown in gray and the long-term reconstructed mean is shown by the dashed line.
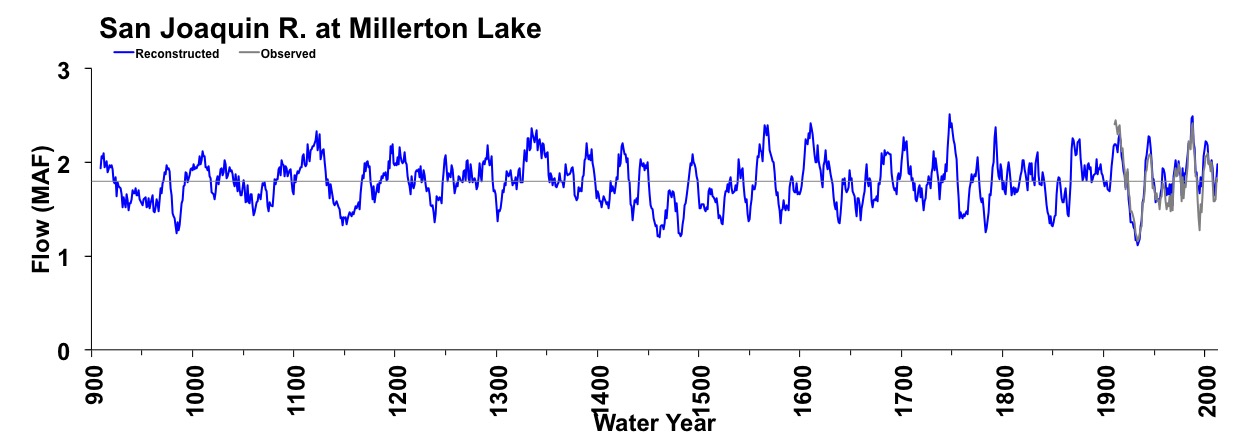
Figure 4. The 10-year running mean (plotted on final year) of reconstructed San Joaquin River flow, 900-2012. Reconstructed values are shown in blue and observed values are shown in gray. The long-term reconstructed mean is shown by the dashed line.



